Coloquios Otoño 2017

Procesos estocásticos en el estudio de la luz

Martes 28 de Noviembre, 14:30 - 16:00, Salón 101

Manuel García Jurado

Resumen: En esta plática veremos cómo el hecho de que la luz interfiere consigo misma se relaciona con los procesos estocásticos en la llamada teoría de coherencia, cómo de la idea del cambio espacial en una correlación obtenemos un resultado polémico para la cosmología, en qué sentido la teoría de coherencia permite la unificación de otras teorías ópticas, y a partir de las características del láser esbozaremos conceptos del aspecto cuántico de la luz.

Sobre la epidemiología matemática en México o cómo NO modelar enfermedades

Martes 7 de Noviembre, 14:30 - 16:00, Salón 101

Rodrigo Zepeda

Resumen: En este coloquio se presentan algunos de los modelos (a veces, "modelos") que se han propuesto en el país para modelar epidemias recientes (dengue, zika, diabetes), así como los problemas asociados desde la recolección de datos (que a veces son de la forma "mi compadre dijo que hay dos casos de chikungunya") hasta la forma de presentarlos. Finalmente, se esbozarán áreas de oportunidad (i.e. qué cosas falta por hacer si esto te interesa).

Reconstrucción matemática de aberraciones ópticas.

Martes 31 de Octubre, 14:30 - 16:00, Salón 101

Claudia García Gil

Resumen:En óptica física, las aberraciones son aquellos defectos o distorsiones en un imagen producidos en un sistema óptico como en prismas, lentes, espejos, etc. Un frente de onda distorsionado puede ser visto como una expansión de un conjunto de polinomios de Zernike sobre una abertura circular. En este coloquio veremos cómo reconstruir un frente de onda distorsionado por medio de estos polinomios así como algunas de sus aplicaciones ópticas en astronomía y medicina.

Sobre nodos y matemáticas

Martes 24 de Octubre, 14:30 - 16:00, Salón 101

Mariana Martínez

Resumen: Los nudos son objetos con que usamos cotidianamente pero su estudio bajo la rama de la topología es bastante reciente. Han surgido varios problemas este estudioejemplos incluyen identificar cuándo un nudo esanfiqueiral, cuándo es primo, si es invertible, cuándo dos nudos son equivalentes, etc.

En este coloquio se estudiarán nudos poligonales y analizará el problema de encontrar invariantes de nudos. En especial se trabajará con el polinomio de Alexander.Veremos cómo llegar a este polinomio de dos maneras distintas: trabajando con determinantes y mediante el procedimiento de Conway.

Modelos lineales generalizados

Martes 17 de Octubre, 14:30 - 15:30, Salón 101

Gian Carlo Diluvi

Resumen: 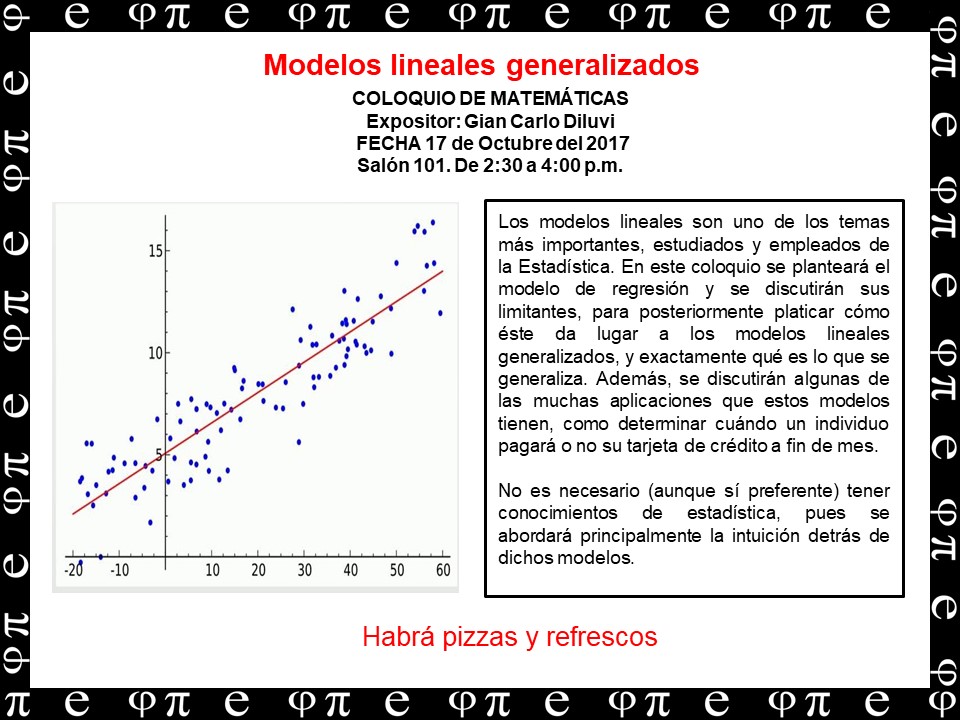Los modelos lineales son uno de los temas más importantes, estudiados y empleados de la Estadística. En este coloquio se planteará el modelo de regresión y se discutrán sus limitantes, para posteriormente platicar cómo éste da lugar a los modelos lineales generalizados, y exactamente qué es lo que se generaliza. Además, se discutirán algunas de las muchas aplicaciones que estos modelos tienen, como determinar cuándo un individuo pagará o no su tarjeta de crédito a fin de mes. 

No es necesario (aunque sí preferente) tener conocimientos de estadística, pues se abordará principalmente la intuición detrás de dichos modelos.

Problemas inversos aplicados a imágenes

Jueves 5 de Octubre, 14:30 - 15:30, Salón 101

Martín Suárez 

Resumen: Los problemas inversos son un área de vital importancia en las matemáticas. En el coloquio nos dedicaremos a revisar el concepto de problema inverso y las problemáticas que surgen en sus soluciones. Luego revisaremos algunas formas de atacar estas problemáticas.

Aplicaremos estos métodos a la eliminación de ruido en imágenes. Veremos cómo llegar del funcional de Tikhonov al método de variación total y una implementación sencilla para la eliminación de ruido.

De paradojas y sonrisas

Martes 12 de Septiembre, 14:30 - 15:30, Salón 101

Concha Ruiz Ruiz Funes

Resumen: Las paradojas matemáticas, además de ser muy divertidas, han llevado a la construcción de conceptos matemáticos muy importantes. Conocerlas puede ayudarnos a entender que en los fundamentos de las matemáticas el camino puede ser maravilloso y peligroso al mismo tiempo.

“Al igual que los buenos trucos de ilusionismo, las paradojas nos causan tanto asombro que inmediatamente queremos saber como se han hecho. Los ilusionistas no revelan jamás sus artes, pero los matemáticos no tienen necesidad de guardar el secreto…”

Kasner y Newman

Curvando el Espacio

Martes 29 de Agosto, 14:30 - 15:30, Salón 101

Ernesto Pérez Chavela

Resumen: La mecánica celeste es una rama importante de las matemáticas que se avoca al estudio del problema de los n-cuerpos y todo lo que esto conlleva, como son colisiones y escapes de partículas, movimientos planetarios, movimiento de satélites y cometas, etc. Todos estos estudios están basados en la ley de atracción universal de Newton, definida en espacios Euclidianos. 

En esta charla hablaré sobre la extensión del problema de los n-cuerpos a espacios de curvatura constante (positiva o negativa), es decir en la descripción del movimineto de n-masas puntuales bajo la acción de un potencial que generaliza al potencial Newtoniano. En particular se mostrará la existencia de un tipo especial de órbitas periódicas donde las distancias mutuaas entre las masas permanece constante para todo tiempo, conocidas como equilibrios relativos, mostrando las diferencias y semejanzas que se tienen con este tipo de movimientos en espacios Euclidianos o espacios de curvatura cero. La charla será motivacional a nivel divulgativo.