Seminarios Primavera 2015
Dinámica de poblaciones y problemas de persistencia para ecuaciones de reacción-difusión
Viernes 15 de Mayo, 13:00 - 14:00, Salón B2
Mario Veruete
Universidad de Montpellier, Francia
Resumen: Las ecuaciones de reacción-difusión aparecen naturalmente en la modelización de procesos tales como reacciones químicas, física de plasmas, morfogénesis , dinámica de poblaciones, entre otras. Hablaremos de ciertos modelos que permiten describir la propagación de una especie y de ciertos criterios espectrales que permiten asegurar la persistencia de soluciones.
Métodos Híbridos para Flujos en Medios Porosos
Viernes 8 de Mayo, 13:00 - 14:00, Salón B2
Dr. Gerardo Hernández Dueñas
Instituto de Matemáticas UNAM - Juriquilla
Resumen: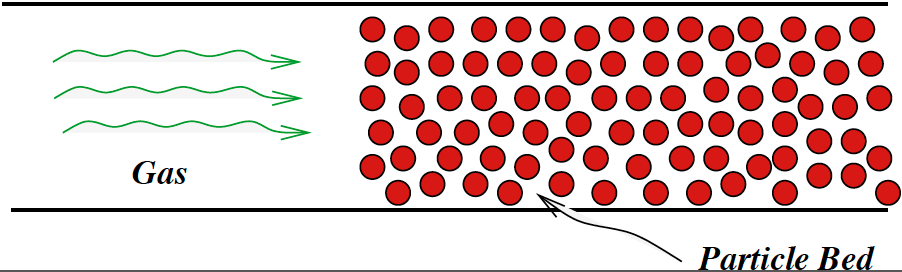 
El modelo de Baer-Nunziato es usado para describir el flujo de un gas compresible en un medio poroso. Estamos interesados en flujos en los cuales la porosidad cambia discontinuamente a través de la “interface”. Un estudio reciente muestra el fallo de varios métodos en el cálculo de la solución correcta cerca de la interface. En este trabajo proponemos un algoritmo híbrido en el cual usamos una formulación no-conservativa a través de la discontinuidad en la porosidad usando la entropía como variable (entre otras). Esta formulación respeta las “invariantes de Riemann” y puede ser combinada con nuestro método numérico conservativo favorito fuera de la interface. En esta plática explicaré en detalle el método híbrido que proponemos y mostraré resultados obtenidos en diferentes problemas de Riemann.
Estudio de patrones organizados de actividad cerebral
Viernes 24 de Abril, 13:00 - 14:00, Salón B2
Dra. Rocío González Ramírez
IFM, Universidad Michoacana de San Nicolás de Hidalgo (Cátedra Conacyt)
![Poster[+]](/sites/default/files/u444/sem150424-poster.png){kind=link}
Resumen:En esta charla panorámica platicaremos de algunos de los enfoques posibles para el estudio del funcionamiento del cerebro usando matemáticas. En la primera parte describiremos el modelo que se considera más importante para el estudio del comportamiento de una neurona, este es el “Modelo de Hodking-Huxley”. En la segunda parte describiremos los llamados “Modelos de Campo Medio”, que se utilizan para describir la actividad en poblaciones de neuronas. Finalmente, describiremos como se pueden usar estos últimos para el estudio de patrones de tipo onda viajera hallados en grabaciones clínicas durante ataques epilépticos.
Viernes 10 de Abril, 13:00 - 14:00, Salón B2
Dr. Jaime Cruz Sampedro
Departamento de Ciencias Básicas - UAM Azcapotzalco
![Poster[+]](/sites/default/files/u444/sem150414-poster.png){kind=link}
Resumen: 
Hace muchos años, frente al Módulo de Mando del Apollo 11 en el National Air and Space Museum un niño de nueve años me preguntó, "¿por qué tiene esa forma?". Sin saber qué responder le dije rápidamente: "porque se ve bonito".
En la búsqueda de una mejor respuesta encontramos que esa pregunta conlleva un problema aerodinámico que Newton investigó en su Philosophiæ Naturalis Principia Mathematica y que, históricamente, es el primer problema del cálculo de variaciones. En su libro, Newton describe geométricamente sendas respuestas para los casos cónico y radial, sin dar ningún indicio de como las obtuvo.
En esta charla presentamos una manera de obtener las respuestas de Newton. En el caso cónico se asoma la razón áurea y el caso radial muestra evidencia que en 1686 Newton entendía las ecuaciones de Euler-Lagrange, desarrolladas alrededor de 1750. Para concluir describimos resultados recientes acerca de la existencia de perfiles aerodinámicos convexos que no poseen simetría radial. Esta charla pretende ser accesible a cualquier estudiante de ingeniería o ciencias exactas de nivel licenciatura.
Superficies de Riemann asociadas a la ecuación no lineal de Schrödinger
Viernes 20 de Marzo, 13:00 - 14:00, Salón B2
Dr. Adrián Espínola Rocha
División de Ciencias Básicas e Ingeniería - UAM Azcapotzalco
Resumen:
Es conocido el trabajo de B. Dubrovin et al. y P. Lax para recuperar las soluciones de la ecuación de Korteweg-deVries (KdV) periódica usando superficies de Riemann. Similarmente, las soluciones de la ecuación periódica No Lineal de Schrödinger (NLS) son encontradas por medio del problema de valores propios de Zakharov-Shabat (ZS).
En esta plática, en vez de trabajar con el problema de valores propios de ZS, trabajaremos con un un problema espectral escalar propuesto por Kamchatnov-Kraenkel-Umarov, recobrando la ecuación NLS y las ecuaciones de orden superior de la jerarquía de Lax. También, daremos una formula general de recursión para obtener sus leyes de conservación.
La charla la iniciaremos con una panorámica sobre las ecuaciones completamente integrables como las ecuaciones de KdV y NLS, así como algunas de sus aplicaciones.
Encontrando y destruyendo ciclos
Viernes 13 de Marzo, 13:00 - 14:00, Salón B2
Dra. Rita Zuazua
Departamento de Matemáticas, Facultad de Ciencias - UNAM
Resumen: El Prof. Carsten Thomassen propuso en los 70's los siguientes dos problemas:
- Una digráfica no hamiltoniana es r-hypohamiltoniana si al eliminar cualquier conjunto de r-vértices se vuelve hamiltoniana. ¿Para qué entero positivo r existen digráficas r-hypohamiltonianas?
- ¿Cuál es el número mínimo de vértices que debo eliminar en una gráfica o digráfica para destruir sus ciclos máximos?
En la plática recordaremos los conceptos necesarios y daremos respuestas a estas preguntas.
¿Qué es la teoría p-ádica de Hodge? Una aplicación a la geometria de superficies K3
Viernes 27 de Febrero, 13:00 - 14:00, Salón B2
Dr. Rogelio Pérez Buendía
IMATE -UNAM / Universidad de Concordia, Canadá
Resumen: 
Uno de los objetivos centrales de la teoría de números moderna es entender al grupo de Galois absoluto de los números racionales G. El acercamiento más importante para lograrlo, es el estudio de las representaciones (continuas) de G, en particular se tiene una clase importante constituida por los espacios vectoriales sobre un campo p-ádico (llamadas representaciones p-ádicas). Dado que el grupo de Galois G está topológicamente generado por sus subgrupos de descomposición G_l con l recorriendo todos los números primos, podemos restringir nuestra atención a las representaciones continuas de estos grupos más simples. Para p distinto de l tales representaciones están bastante bien entendidas pues en estos casos, el requisito de continuidad limita de manera drástica el tipo de representaciones que se pueden tener. Para l = p, sin embargo, la situación es mucho más rica e interesante.
El objetivo de la teoría p-ádica de Hodge es clasificar y estudiar a las representaciones p-ádicas de G_p (es decir con p = l) y lo ha logrado con gran éxito. Mucha de la teoría ha sido motivada por el estudio de las representaciones de Galois que provienen de la geometría (vía la cohomología étale) por lo que no es una sorpresa que la teoría p-ádica de Hodge tenga importantes aplicaciones a aritmética.
En esta plática daré una visión general de la teoría p-ádica de Hodge haciendo algunas comparaciones con la teoría de Hodge clásica para variedades complejas. Motivaremos su importancia ilustrando una aplicación al estudio de las superficies K3 definidas sobre un campo p-ádico.
Matemáticas, Física e Ingeniería de MEMS y NEMS
Viernes 20 de Febrero, 13:00 - 14:00, Salón B2
Dr. Raúl Esquivel Sirvent
Instituto de Física - UNAM
Resumen:
Los micro y nano sistemas electromecánicos son ya tecnología de uso común. Pese a su simplicidad hay problemas fundamentales y es un área activa de investigación en las matemáticas, la física e ingeniería. Esto presenta una visión poco antes vista de cómo cada una de estas áreas ataca un mismo problema.
En esta plática discutiré problemas de estabilidad en la solución de las ecuaciones diferenciales que describen los MEMS/NEMS. A escalas del orden de 100 micras fuerzas de origen cuántico como las de van der Waals y Casimir aparecen y cambian la estabilidad de estos sistemas. Los modelos matemáticos y físicos utilizados son idealizados pero permiten una descripción correcta de los MEMS y NEMS. La validez de los resultados se discute en relación al diseño y fabricación de estos dispositivos.
Inestabilidades en el Sistema Solar: el caso de los Kirkwood gaps
Viernes 13 de Febrero, 13:00 - 14:00, Salón B2
Dr. Pablo Roldán
Department of Mathematics, University of Maryland at College Park
Resumen: 
La estabilidad del Sistema Solar es un problema muy antiguo. A lo largo de los siglos, matemáticos y astrónomos han intentado demostrar teoremas de estabilidad cada vez mas fuertes para sistemas dinámicos relacionados con el Sistema Solar usando el modelo Newtoniano de N-cuerpos. Un resultado clave en esta dirección es el teorema de Arnold, que prueba la existencia de un conjunto de medida de Lebesgue positiva ocupado por toros invariantes en los sistemas planetarios, siempre que la masa de los planetas sea pequeña. Aun así, en el espacio de fase los huecos entre toros invariantes dejan espacio para inestabilidades. En realidad, los cálculos numéricos de Sussman, Wisdom y Laskar han mostrado que a lo largo de la edad del Sol, son probables las colisiones y eyecciones de planetas interiores. Actualmente el punto de vista imperante es que nuestro Sistema Solar es inestable, y la conjetura general sobre el problema de N-cuerpos es casi opuesta a la que antes era: no se cumple ningún tipo de estabilidad topológica, en un sentido muy fuerte. (Herman lo llamó "el problema abierto más antiguo en sistemas dinámicos".) Nuestro resultado, muestra la existencia de inestabilidades globales en un sistema sistema planetario realístico (el problema de tres cuerpos Sol-Júpiter-Asteroide) y describimos el mecanismo de inestabilidad asociado. Por tanto damos un paso hacia la prueba de la conjetura de Herman. Estas inestabilidades ocurren cerca de las resonancias de tipo mean motion. Esta es la primera vez que se han establecido inestabilidades globales en un sistema planetario realístico. Si el tiempo lo permite, también explicaré la relación entre estas inestabilidades y la existencia de los llamados Kirkwood gaps, huecos en la distribución de asteroides en el Cinturón de Asteroides.
De la formación de patrones en algunos procesos naturales; el encuentro de dos teorías
Viernes 6 de Febrero, 13:00 - 14:00, Salón B2
Dr Víctor Breña Medina
Centro de Ciencias Matemáticas, Morelia - UNAM
Resumen:
En la naturaleza existe un amplia diversidad de fenómenos que escapan de nuestra completa compresión. Por ejemplo, la predicción del clima y las epidemias de dengue e influenza, o bien, el crecimiento de tumores o el hecho que todos los mamíferos tienen cinco dedos en su estructura ósea.
El entendimiento de los fenómenos naturales requiere de la compresión del involucramiento de procesos físicos, biológicos y químicos, donde éstos participan en distintas escalas espaciotemporales. Las teorías matemáticas permiten el discernimiento de estas escalas y su participación en los fenómenos que ocurren en la naturaleza. De esta manera, las matemáticas y las otras disciplinas de la ciencia se complementan transversalmente.
En esta plática presentaré algunos rasgos de la teoría de formación de patrones donde dos procesos físico-químicos juegan un papel fundamental en la biología: la reacción y difusión de sustancias. Para ello echaré mano de las ecuaciones de reacción-difusión, las cuáles han mostrado particularmente ser de utilidad en el estudio de fenómenos biológicos. Primero, explicaré brevemente las ideas de Alan Turing, mejor conocidas como 'bifurcación de Turing’; asimismo, haré lo correspondiente con la teoría conocida como 'serpenteo homoclínico’. Comparando estas dos teorías, mostraré algunas de las características teóricas que son indispensables para la modelación de procesos biológicos. Además, mostraré superficialmente una de las consecuencias de esta convergencia de teorías conduce a una descripción del proceso de iniciación de 'pelos radiculares' en raíces de plantas; éstas son células clave para la toma de nutrientes y anclaje. El proceso de iniciación se cree puramente genético, sin embargo el resultado que en esta plática presento, sugiere la participación primordial de características físicas usualmente no consideradas por investigadores experimentales.
Viernes 23 de Enero, 13:00 - 14:00, Salón B2
Dr. Ramón G. Plaza
Instituto de Investigaciones en Matemáticas Aplicadas y Sistemas - UNAM
Resumen:
En esta charla se discutirá la existencia y estabilidad de ondas viajeras o frentes para sistemas de ecuaciones de tipo hiperbólico que modelan reacción-difusión, conocidos como sistemas de tipo Cattaneo-Maxwell. El término de reacción considerado es de tipo biestable. Éstos sistemas fueron introducidos para remediar la velocidad de propagación infinita que caracteriza a la ecuación de reacción-difusión standard. Para ello, se modifica la ley de Fick por una ecuación de evolución para el flujo con un tiempo de relajación suficientemente pequeño. El resultado es un sistema hiperbólico que modela reacción-difusión. Se discutirá la existencia de frentes de onda y su estabilidad. En particular, ésta última involucra técnicas de función de Evans para analizar la estabilidad de tipo espectral. La información espectral es crucial para demostrar que las ondas son nolinealmente estables bajo perturbaciones pequeñas. Éste es un trabajo en colaboración con C. Mascia (Roma), C. Lattanzio (L'Aquila) y C. Simeoni (Niza).
Preservación de volúmenes en mecánica no-holónoma
Viernes 16 de Enero, 13:00 - 14:00, Salón B2
Dr. Luís García Naranjo
Instituto de Investigaciones en Matemáticas Aplicadas y Sistemas - UNAM
Resumen: En mecánica, las restricciones en las configuraciones de un sistema se denominan “holónomas”. Un ejemplo sencillo es la longitud constante del péndulo. Sistemas mecánicos con restricciones en las velocidades que no pueden reducirse a restricciones en las posiciones se llaman “no-holónomas”. Un ejemplo clásico es una esfera que rueda sin resbalar en una mesa.
El reto en el estudio de los sistemas mecánicos no-holónomos aparece debido a que las ecuaciones de movimiento no poseen una estructura Hamiltoniana. Sin embargo, la dinámica del sistema puede ser descrita en términos de un corchete de funciones que no satisface la identidad de Jacobi. Hablamos entonces de una “corchete casi-Poisson”. La pérdida de la identidad de Jacobi da lugar a fenómenos que no son posibles en los sistemas Hamiltonianos clásicos. Algunas preguntas abiertas en el área de mecánica no-holónoma incluyen determinar condiciones para la existencia de una medida conservada, existencia de equilibrios asintóticos, relación entre simetrías y leyes de conservación, reducción e integrabilidad. En la primera parte de la charla presentaré una introducción básica a los sistemas no-holónomos rica en ejemplos. Después procederé a presentar un trabajo reciente en conjunto con Y. Fedorov y J.C. Marrero en donde estudiamos el problema de la preservación de una medida para sistemas no-holónomos con simetrías de una manera sistemática. Nuestro método nos permite identificar valores de los parámetros para los cuales existe una medida invariante para sistemas mecánicos concretos.
Síguenos en:
